This is the final version of the term paper I wrote for my Psych 301 class, "The Psychology of Learning." It is shorter and more narrowly focused. It is 13 pages, not including the title page and references. It does have an extra section about the emergent nature of the power function. So, I shaved off about 4 pages and added one. I have not combined these two papers because I want these posts to accurately reflect what I actually turned in for a grade.
A Brief History of the Mathematical Definition of Forgetting Curves
by Grant S. Robertson
Written July, 2008
When attempting to investigate learning, it is unfortunate that scientists are as of yet unable to take direct measurements, within the brain, of how much has actually been learned at a given point. Indirect measures must instead be used to determine what has been learned, or – more importantly – what has been retained. As is common knowledge, the amount retained appears to decrease over time. (Ebbinghaus, 1885) For most of history, this fact has been either not given much thought or discussed in purely qualitative terms. However, in about 1879 Herman Ebbinghaus began a six-year research project where he devised tests to quantitatively measure retention under various conditions. In 1885, Ebbinghaus published a book wherein he described how he performed his tests and even explained his method of statistical analysis.
Ebbinghaus discovered that retention falls off quickly at first and then more slowly later, in a pattern that has since been referred to alternatively as a “forgetting curve,” “forgetting function,” “retention curve,” or “retention function.” In the 123 years since the publication of Ebbinghaus's work there has been much research done on the nature of these "forgetting curves" and what affects them. After firmly establishing that the amount of material retained in memory does, in fact, follow a curve which is steeper at first and shallower later (e.g. Wylie, 1926; Boreas, 1930; MacLeod, 1988), researchers turned their attentions to determining an exact equation to express the nature of this curve (e.g. Wherry, 1932; Murdock, 1960; Wickelgren, 1974; Rubin & Wenzel, 1996) in a mathematical process called “curve fitting.” Different primary mathematical functions have been attempted, from Ebbinghaus’s first logarithmic function (1885) to exponentials (Murdock, 1960) and power functions (Wickelgren, 1974). After over a hundred years, one enterprising pair of researchers undertook the arduous task of performing a curve fitting analysis for over 210 different data sets, matching each of them to 105 different two-parameter functions (Rubin & Wenzel, 1996). They determined that three different basic functions performed equally well. A further review of what has become known as the “Wickelgren Power Law” (Wixted & Carpenter, 2007) reveals that it not only can be made to fit the existing data but can accurately predict later data-points when given only the first few. As any scientist will tell you, the ability to predict future results is the calling card of a good theory.
The Discovery of Forgetting Curves and Early Research Supporting the Concept
Herman Ebbinghaus (1879 – 1885)
In 1879 Herman Ebbinghaus began his landmark study attempting to quantify memory which he defined “in its broadest sense, including Learning, Retention, Association and Reproduction” (Ebbinghaus, 1885, Preface). In 1885 he published a book of his research called, “Memory: A Contribution to Experimental Psychology” and what a contribution it was. In nine chapters, Ebbinghaus discussed the qualitative nature of the, then current, thinking on the subject, then moved on to provide details on the experiments he performed. In his experiments, Ebbinghaus – using himself as his only subject – would memorize a list of nonsense syllables to the point where he could repeat them twice. Then, depending on varying conditions, attempt to relearn that same list to the point where he could repeat it twice again. This technique was devised to remove ambiguity from his research. Rather than simply asking (himself) how many items from a list he could remember – which he determined to be an unreliable means of measuring retention – he used the savings in time necessary to relearn the lists as a measure of how much had been retained. He used these techniques to test for retention as a function of a variety of different conditions, each described in its own chapter.
The chapter most important for this review is “Chapter 7. Retention and Obliviscence as a Function of the Time.” “Obliviscence” simply means “Forgetting” (A Dictionary of Psychology, 2001 cited in encyclopedia.com, 2008). In this experiment, Ebbinghaus attempted to determine exactly how much he could remember after a given period of time (§ 27). In order to avoid the confounding variable of practicing the same list over and over again, he learned 163 different lists with 13 syllables each and only attempted to learn each list twice: once as the original learning and once at a predefined time after that original learning. He divided the 163 lists into eight different groups and attempted the second learning after a different delay for each group (§ 27). So, after lots of exhausting tests and a bit of adjustment for different conditions, Ebbinghaus arrived at the following simple chart depicting how much he tended to retain after a specific period of time:

Though Ebbinghaus discussed the “curve” produced when these figures are plotted, he never produced an actual plot of the data. Following is a plot of this data created in Microsoft Excel. The smooth curve in the plot is a result of the smoothing feature of the software. Only the actual data points from the table above are of importance.

You may notice that the forth data point is slightly higher than one might expect if memory behaved in a smoothly progressing fashion. Ebbinghaus discusses this in Section 29.2 and attributes it to possible errors in his methodology or the exercise thereof. All-in-all, this plot of the first “forgetting curve” in history is still quite telling. It reveals how retention falls off quickly at first and then shifts to falling off quite slowly. From the curve seen above it is difficult to ascertain whether the actual amount of material retained would drop all the way to zero or would asymptote on some positive, non-zero number.
Groundbreaking as it was, Ebbinghaus’s study was not without its critics. One-hundred years after the publication of Ebbinghaus’s book, Henry L. Roediger summarized these criticisms thus, “First, he employed only one subject-himself. Second, and a more common criticism today, is that the artificiality of Ebbinghaus's experimental conditions guaranteed that nothing important or useful could be found from his research. His research and the tradition it spawned is alleged to lack external validity.” (Roediger, 1985) Though, Roediger’s criticisms do have merit, this author believes it is a bit of an overstep to claim that the entire tradition spawned by Ebbinghaus lacks external validity. The work of Ebbinghaus was a starting point. In the over 100 years since, a great deal of good research has been done to expand on what Ebbinghaus started and to bring it into the real world through practical application.
Follow-up Studies on Forgetting Curves
In 1917 Margaret Wylie began a study wherein she used Chinese symbols to test retention. Rather than learning to recite the symbols or recall them when questioned, the Wylie study merely tested whether participants could recognize the symbols they had seen in the past. Wylie found that the ability to recognize symbols followed the same type of curve that Ebbinghaus observed for relearning nonsense syllables (Wylie, 1926). Th. Boreas published a study in 1930 in which he replicated Ebbinghaus’s work with the addition of using verses instead of nonsense syllables and over a much longer period of time. He found that retention for verses parallels that of nonsense syllables although the slopes in both the short and long terms are shallower. In one case Boreas observed that absolutely none of the original learning for nonsense syllables could be detected after a 10 month period (Boreas, 1930). This may indicate that the forgetting curve does asymptote to zero after all.
A. R. Gilliland tested to see if the Ebbinghaus forgetting curve applied to more real world material. Gilliland used a series of picture cards depicting a complex office scene. Participants were given 30 seconds to study the image and then were immediately asked to recall as much as possible. The quantity of material recalled was used as a baseline for later trials. Gilliland found that initial retention did not fall off as quickly as Ebbinghaus had observed. Gilliland concluded that Ebbinghaus was far too pessimistic in his estimation of how fast retention initially falls off and attributed this to Ebbinghaus’s use of nonsense syllables rather than real world material (Gilliland, 1948). In the end, though, the results Gilliland obtained did reflect more rapid fall off of retention nearer to the original learning than later, thus confirming the crux of the work Gilliland contends to refute.
The forgetting curve has also been explored in the context of witness viability (Deffenbacher, Bornstein, McGorty, & Penrod, 2008). In their meta-analysis of 53 other studies, the researchers determined that retention and recognition of human faces fell off at a rate that matched that described by the Wickelgren Power Law, a function which accurately describes the Ebbinghaus forgetting curve and will be discussed later in this review. Other contexts that have been studied are remembering pictures (MacLeod, 1988), visual memory decay (Gold, Murray, Sekuler, Bennett, & Sekuler, 2005), and even marijuana use (Lane, Cherek, Lieving, & Tcheremissine, 2005).
Finding a Mathematical Definition Through Curve Fitting
Once it had become firmly established that the curve of forgetting did, in fact, follow the same path first described by Herman Ebbinghaus in 1885, researchers began to look for an equation – with a theory to back it up – which accurately expressed the nature of this forgetting curve while allowing for all the variations due to context and material that had been observed over the years. Researchers devised various equations and used curve-fitting (a mathematical process by which parameters of an equation are adjusted until the equation most closely matches the available data) to test these equations against their data.
Ebbinghaus made the first attempt at curve fitting, though he did not call it that, in his book. He devised a logarithmic equation that closely fit the data from his original experiment: b = 100k/((log t)c + k) where b is percent retained, t = time since original learning, and c and k are constants: k = 1.84 and c = 1.25 (Ebbinghaus, 1885, § 29.3). He then created the chart comparing the observed and calculated values shown below:

In order to make these numbers easier to understand a plot of them has been created in Microsoft Excel and is presented below:
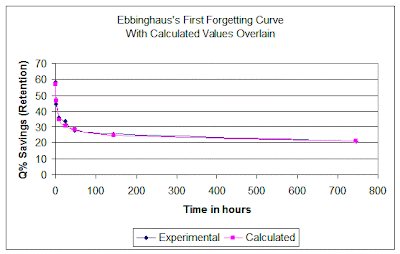
Notice how closely the calculated values follow the observed values with the exception of the forth data point discussed earlier.
Further attempts at finding a mathematical expression to define the forgetting curve were hit and miss for a while, as were the theories that accompanied them. Matthew N. Chappell of Columbia University presented an interesting theory that because learning involves a transfer of energy and that energy begins being dissipated right from the beginning then the forgetting curve must necessarily follow a logarithmic function (1931). After extensive searching of the CSA Illumina aggregated database of research articles using search terms such as “AB=forgetting and AB=(curve* or function or functions) AND AB=(mathematical or (curve NEAR (fit or fitting))” no further attempts to express the forgetting curve mathematically could be found up until 1960. At that time, Murdock and Cook published “On fitting the exponential” where they endeavored to educate the Psychology community about the mathematical methods of curve fitting using the exponential as an example(1960). In 1971 a Czech researcher did a review of attempts to mathematically model learning from 1962 to 1971 (Brichacek, 1971) however the full text of the article was not available. This reviewer can only surmise that either not much thought was given to finding an accurate function up until the 1960s or that earlier researchers merely assumed the Ebbinghaus formula was correct.
The Wickelgren Power Law
Wayne Wickelgren, according to Wixted and Carpenter, “studied the time course of forgetting more assiduously and more effectively than anyone since Hermann Ebbinghaus” (Wixted & Carpenter, 2007, p. 133). In 1972, Wickelgren published a major study which included his Strength-Resistance Theory, a mathematical theory based on the logarithm which he claimed accounted for many different aspects of the forgetting curve and how it varies depending on subject matter and context. Wickelgren also presented a considerable body of research illustrating how well his theory matched the data (Wickelgren, 1972). However, just two years later he published his groundbreaking “Single-trace fragility theory of memory dynamics” (Wickelgren, 1974). In this theory, Wickelgren refuted the notion that short-term memory is separate from long-term memory and instead proposed a mathematical theory which encompassed them both. This theory claims that a memory “trace” (a term used by Ebbinghaus (1885, § 26)) can be described by a series of equations that include both an exponential and a power function. A mathematical explanation of these equations is outside the scope of this review (see Wickelgren, 1974, 775-776). For those of us who are not experts in calculus and differential equations, a better – though still not entirely simple – explanation of the math behind this theory can be found in Wixted and Carpenter’s “The Wickelgren Power Law and the Ebbinghaus Savings Function” (2007).
One of the main tenets of this new theory is that the forgetting curve is affected by two primary parameters: the strength of the memory trace and its fragility. Strength refers to the degree of learning associated with a particular memory. Whereas fragility refers to the difficulty the mind will have in retaining that memory over time. If one studied a long series of nonsense syllables until one could recite them easily multiple times the memory trace would likely be characterized by a high degree of strength during the recitations. However it would suffer from a high degree of fragility because there is nothing on which to attach the memory within long term memory and the nonsense syllables have no value for the individual. On the other hand, an important conversation with a loved one might have a memory trace characterized by low strength and low fragility. One might not remember the exact words after just an hour but one would remember the gist of the conversation for perhaps a lifetime. The third parameter is a constant which has yet to be determined. Its purpose is to account for the fact that we measure time in arbitrary units to which brain cells do not adhere. The final parameter is simply the time since the original or most recent learning period.
This reviewer finds Wickelgren’s theory quite compelling not only because it has a simple logical explanation but because it matches the data so very well. In “One hundred years of forgetting: A quantitative description of retention,” Rubin and Wenzel analyzed 210 different data sets and attempted to curve fit each of 105 different two-parameter equations (1996) — not including the additional parameter of time. They made sure to include equations that had been suggested by researchers but also included some relatively random equations just to see what would come up. In the end they presented three different equations as having the most promise: a simple power law, the hyperbola-in-the-square-root-of-t forgetting function (which had never been proposed before), and what they called the “Rubin-Wenzel-Wickelgren-Weibull-Williams-Watts exponential-power law” (p. 758). It is the review of Wickelgren’s work done by Wixted and Carpenter (2007) that is the most convincing. Not only do they clearly explain the logic behind Wickelgren’s theory, but they illustrate how the equation accurately predicts latter data points when only given the first few. As the authors state, this is a much stronger indication of the accuracy of a formula than simply being able to be fit to a complete set of points (p. 133).
Below is reproduced Figure 1 from Wixted and Carpenter’s 2007 paper. In this graph, Wixted and Carpenter use the data from the original Ebbinghaus results and attempt a curve-fitting with both the Wickelgren Power Law and a simple exponential function. You may recognize these data points from the Excel plot presented earlier.

As the caption says, even when only the first five data points are used in the curve-fitting process, the Wickelgren Power Law accurately predicts the last data point even though Ebbinghaus, himself, admitted that the forth data point must be in error (Ebbinghaus, 1885, § 29.2). In fact, when multiple different curve-fittings are overlain on one another, it is almost impossible to discern a difference between them. Pay close attention to the thickness of the plot at the top compared to the bottom. It is slightly thicker at the bottom indicating that the plots don’t line up exactly, but are very close. Compare this to the curve-fitting of a simple exponential to the same data using the same procedure: first with only the first five data points then with one more for each iteration of the process. Notice how the curves produced (though they look like straight lines) do not even intersect the last two data points as oversized as they are. Also notice how the line moves dramatically with each additional data point that is considered. It should be noted that the simple exponential function was not one of the top three functions selected by Rubin and Wenzel (1996) and that none of the other top candidates were analyzed in this manner by Wixted and Carpenter. It would be interesting to see just how well the other two functions stack up against the Wickelgren Power Law under the same graphical analysis.
“The Power Law” as an Emergent Property
An “emergent” property is a property or characteristic that appears only when other more fundamental properties or aspects of a phenomenon are combined. For instance, each water molecule in a lake has a mass and velocity, along with the quantum forces that keep the molecules from getting too close or far away from each other. It is the combined movement of all those individual molecules in a lake or ocean that create the waves and currents that we see. In the same way, it has been shown that the Wickelgren Power Law may likely be the result of a combination of many more fundamental phenomenon acting in concert.
Drawing on the work of Rubin and Wenzel (1996), Sverker Sikström of the University of Toronto used advanced mathematical modeling and simulation to show that power functions appear when multiple different exponential curves are combined. He made what he claims are biologically sound assumptions: that learning rates will vary slightly over time, that individual parts of the system (e.g. brain cells) will have varying effects, or “weights” within the system, and that those weights will have “bounds” or limits on their total effect within the system. Sikström concluded that the power function is a natural result of the combined effect of all the brain cells participating in a network involved in learning a particular thing. These individual brain cells behave in an exponential manner but their combined activity produces the emergent property of the power function for the network as a whole (1999). Additionally, Sikström makes the flat statement in his abstract that “Empirical forgetting curve data have been shown to follow a power function” (1999, p. 460).
Soon after Sikström presented his paper, Richard Anderson of Bowling Green State University did additional work showing that the power function could appear emergently from the combination of many different more fundamental functions. Anderson also simulated the forgetting process using a computer. However, he used range-limited linear functions, range-limited logarithmic functions, basic power functions as well as basic exponential functions as the assumed function for each individual simulated brain cell in the network. He found that the power function emerged most strongly when the variability between the different “cells” in the network was highest in almost all cases. The only exception was when the basic function was already a power function, in which case the simulation always resulted in a power function regardless of variability. Anderson concludes by speculating that the power law, rather than being ubiquitous because it is a fundamental biological property of brain cells, is ubiquitous simply because it the mathematical result of combining many different response curves with a high degree of variability between them (2001).
Conclusion / Discussion
In the hundred-odd years since Herman Ebbinghaus did his first experiments, using savings in learning time as a measure of retention, and made his first attempts at formulating a mathematical function that could describe the forgetting curve he obtained, much research has been done to both verify Ebbinghaus’s findings and to perfect an equation to describe that curve. Many functions have been theorized, and one has been found to both fit the available data and predict future results accurately. Though no wide-spread, unanimous support was found for the “Wickelgren Power Law,” a preponderance of the articles that were discovered seemed to take “the power law” as a given and use it as the basis for further research. In addition, the power law may not be a fundamental property of the nature of learning. However, as a rather ubiquitous emergent property, it will likely be possible to use it as the basis around which to devise learning and education systems.
References
Anderson, R. B. (2001). The power law as an emergent property. Memory & Cognition, 29(7), 1061-1068. Retrieved from www.csa.com
Brichacek, V. (1971). Mathematical models of learning: II. Ceskoslovenská Psychologie, 15(2), 144-157. Retrieved from www.csa.com
Boreas, T. (1930). Experimental studies on memory. II. the rate of forgetting. Praktika De l'Académie d'Athènes, 5, 382 ff. Retrieved from www.csa.com
Cepeda, N. J., Pashler, H., Vul, E., Wixted, J. T., & Rohrer, D. (2006). Distributed practice in verbal recall tasks: A review and quantitative synthesis. Psychological Bulletin, 132(3), 354-380. Retrieved from http://content.apa.org/journals/bul/132/3
Chappell, M. N. (1931). Chance and the curve of forgetting. Psychological Review, 38(1), 60-64
Deffenbacher, K. A., Bornstein, B. H., McGorty, E. K., & Penrod, S. D. (2008). Forgetting the once-seen face: Estimating the strength of an eyewitness's memory representation. Journal of Experimental Psychology: Applied, 14(2), 139-150
Dictionary of Psychology, A. (2001). Retrieved July 2, 2008 from http://www.encyclopedia.com/doc/1O87-obliviscence.html
Ebbinghaus, H. (Ruger, H. A. & Bussenius, C. E., Trans. 1913). Memory: A contribution to experimental psychology. New York, NY, US: Teachers College Press. (Original work published 1885)
Gold, J. M., Murray, R. F., Sekuler, A. B., Bennett, P. J., & Sekuler, R. (2005). Visual memory decay is deterministic. Psychological Science, 16(10), 769-774
Lane, S. D., Cherek, D. R., Lieving, L. M., & Tcheremissine, O. V. (2005). Marijuana effects on human forgetting functions. Journal of the Experimental Analysis of Behavior, 83(1), 67-83
MacLeod, C. M. (1988). Forgotten but not gone: Savings for pictures and words in long-term memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 14(2), 195-212
Murdock, B. B. Jr., & Cook, C. D. (1960). On fitting the exponential. Psychological Reports, 6, 63-69.
Roediger, Henry L.,III (1). (1985). Remembering Ebbinghaus. US: American Psychological Association
Rubin, D. C., & Wenzel, A. E. (1996). One hundred years of forgetting: A quantitative description of retention. Psychological Review, 103(4), 734-760
Sikström, S. (1999). Power function forgetting curves as an emergent property of biologically plausible neural network models. International Journal of Psychology.Special Issue: Short-term/working Memory, 34(5-6), 460-464
Wickelgren, W. A. (1974). Single-trace fragility theory of memory dynamics. Memory & Cognition, 2(4), 775-780. Retrieved from www.csa.com
Wixted, J. T., & Carpenter, S. K. (2007). The wickelgren power law and the ebbinghaus savings function. Psychological Science, 18(2), 133-134
Wylie, M. (1926). Recognition of chinese symbols. American Journal of Psychology, 37, 224-232
This post is Copyright © 2009 by Grant Sheridan Robertson.
How does the law's control variable change with age
ReplyDeleteTo tell you the truth I have no idea. I don't know if any research has been done on that possibility at all. Wickelgren appeared to believe that it was simply a constant that gave a number to something that had no concept of numbers, the rate of chemical reactions in brain cells. Similar to the way the gravitational constant gives a number to physical forces that have no concept of numbers.
ReplyDeleteI can send you the full .PDF files of the Wickelgren 1974 Single-trace fragility theory... and the Wixted & Carpenter 2007 The wickelgren power law... papers if you want. Just contact me through the address in my profile.
The purpose of my review was to show that there was an acceptable forgetting curve function that could be used in software designed to increase retention of information by use of spaced repetition. My teacher had already forced me to cut my review shorter than I had wanted, so delving into the specifics of whether that constant changed with age would have been way beyond the scope of my review.
My personal suspicion is that it would be very difficult to tell whether that constant was changing or if the other major factors, strength and fragility, were doing the changing instead. For mathematical purposes it should be possible to choose a value for the constant that puts the strength and fragility values within a reasonable range for analysis, and then simply lock it there.
The absolute values of the strength and fragility are unimportant. Only the relative values from one time to another for a single memory or the differences between one memory and another. Just like any other measurement system, the absolute values only take on meaning when compared to other things measured by the same system.
Hey, thanks! Your work helped me find out what has been said on power law forgetting.
ReplyDeleteI have 2 questions here in regarding to Wixted & Carpenter (2007). First, in Eq 1, physio- factors such as age should be included in "psi", the rate of forgetting. Thus, "psi" becomes a function capturing certain physio-factors. Does it make sense?
ReplyDeleteSecond, certain texts present the dependent variable, m, as the number of, say, the words the subject can recall. Yet when m is presented as the proportion of learning materials the subject can recall, the y-intercept has to be 1 (100% since everything must be recalled at t=0)and so it restricts lambda being 1. As as such, degree of learning is one?
(Response in multiple posts due to 4096 character limit in Blogger.)
ReplyDeleteAnonymous,
Please remember, I wrote this paper for an undergraduate psychology class a few years ago. I have yet to complete my bachelor's, this blog is the only place this paper has been "published" and it certainly has NOT been peer reviewed. So I may not be the best reference on this topic. On top of that, I do not pretend to completely understand all the math behind Wickelgren's power law, expressed in Equation 1 of Wixted 2007. That said, I will attempt to answer your question anyway. Take it for what it is: a guess based upon my reading of the paper.
Assuming you have access to the Wixted paper: It seems that aging factors would be incorporated into psi as having a direct effect on the rate of forgetting.
I believe Beta is merely a "scaling factor" for time - as Wixted states - in that it stretches out (or compresses) the forgetting curve along the x-axis (or time-axis in this case) merely to make the graph easier for humans to interpret. Remember, the units we use for time are entirely arbitrary. Chemicals in your brain cells do not know what a second or a minute is. If your experiment is measuring the rate of forgetting in seconds then you would have a really long graph for a two-week old memory. But if you multiply the number of seconds by 1/86400 then you will show the graph in terms of days resulting in a graph that is 14 units long, a much more manageable number. Remember also, that when one multiplies any independent variable which is also used as one of the axis of the graph, all that EVER does is scale the graph itself.
As to the units used for m, lambda, and psi: Naturally one would want to ensure that the units were consistent across all variables. Other than that, I couldn't tell you for sure.
(Continued from previous comment)
ReplyDeleteI believe your are making an incorrect assumption in your second question. Remember m is a prediction of memory strength at some time t > 0. Lambda is the strength of the memory at t = 0 but we can't test that value independently without actually changing it. Lambda can only be ascertained right at the end of a period of study. You assume that "everything must be recalled at t=0" but this does not take into consideration several important factors:
A) The subject may not actually remember 100% of the material even right after studying it. (Don't you wish you could remember everything you tried to learn after studying it for the first time.) Many experiments do not require the subject to study till they have 100% recollection because the purpose of all this work is to find a way to increase the amount of learning over the SAME period of time. So researchers often allow only a certain period of time for subjects to study. Thus the subjects do not have 100% recollection at t=0.
B) Even if subjects do study to 100% recollection, it is possible - and entirely likely - that most of what they are recalling at that time is actually in short-term memory rather than long-term memory. (Of course the word "in" here is a misnomer. Memories don't actually get moved from one type of memory to another. They are merely reinforced to the point of becoming long-term right where they sit. For an explanation of how this works please see my paper "Spaced Repetition for Learning Concepts: A new neurobiological foundation for research and a computer-aided means of performing said research" starting at http://www.ideationizing.com/2010/11/span.html#neurobiology.) Therefore, what may appear to be a memory with 100% strength may actually be merely 10% depending on how long and in what manner the material was originally studied.
C) Every time you test for m you actually change lambda and psi. Yes, testing memories usually reinforces them, especially if they are tested in particular ways or at particular time intervals (again, see my other paper). So the equation is actually an iterative one. Once you test for m you must reset the clock to t=0, lambda gets hiked up a bit over the the m value you just got in the test because the memory is now stronger after the test than it was just prior to the test, psi is now lower because the memory is less fragile (as described in Wickelgren, 1974), and you start the process all over again. Ebbinghaus controlled for this by memorizing many different sets of nonsense-syllables and testing for each only once. So, each different data point you see in the famous Ebbinghaus forgetting curve is an m value from an entirely different list. Ebbinghaus merely assumed he had memorized each list to identical strength and fragility, thus allowing him to assume that each list would have the same forgetting curve in his brain. This is just like when doing research on live animals when one has to remove organs to test the progress of the experiment. Removing the organ definitely alters the progress of the experiment in that particular animal (it usually kills the animal) so researchers must use many different animals from which they remove organs at different times within the experiment. All the results are then graphed on one graph as if the researchers had been able to track the progress of the experiment through one amalgamated animal.
(continued in next comment)
(Continued from previous comment)
ReplyDeleteSo, even though you may think lambda is 1 it may be far from it. Lambda is merely an estimated value based on the previously tested for m. I don't think anyone has figured out how to best estimate lambda and psi. I am sure it depends on previous values of m, gathered from previous tests. However, as I stated above, if one is testing the same memory then one must also account for the fact that lambda and psi will be moving targets. Remember, in Wixted's paper he used the first five values for m in Ebbinghaus' experiment and used curve fitting to determine what the average lambda and psi were for all those five distinctly different memories in Ebbinghaus' brain. Only then was Wixted able to predict the following three values of m using the derived values of lambda and psi. The task would be much more difficult, if not impossible, when using only one or two values of m for the curve fitting.
I imagine, in the real world, using software based upon the DEMML standard (www.demml.org), one could estimate lambda and psi based on the lambda and psi values for other, similar memories. Naturally they are going to be slightly different for each memory for each person simply because they are based on the strength, life time, and number of synapses involved with any particular memory in any particular person's brain. Anyone who is looking for the ONE universal lambda and psi is chasing a rainbow.
For further information, perhaps you should simply contact John Wixted himself. He still teaches at University of California in San Diego. His web site is at: http://wixtedlab.ucsd.edu/index.php?id=wixted.html
If you don't have copies of the Wixted or the Wickelgren papers I cited, I will be happy to send them to you (along with everything else I have). Just e-mail me through the link in my profile.
Good luck in your research,
Grant S. Robertson
Thank you very much Grant. Actually I'm a PhD student in econometrics working on my thesis on inflation expectations of survey data. Part of my thesis is that I attempt to show that, from the cognitive psychological perspective, when being surveyed, consumers do not behave like econometrician, trying to forecast future inflation rate statistically. In fact, they may heuristically calculate the inflation rate from the prices they remember such as the prices of milk, bread, etc, when they shopped in supermarkets. Here I assume that, by setting "m" as the proportion of pieces of information the subject can recall, "m" can also be interpreted as the probability the subject can recall the price of a particular good.
ReplyDeleteI'm now trying to incorporate certain psychological theories into the forgetting curve; the first one I'm considering is the spreading activation theory. Here's what I think (please give me some comments). Say, from the forgetting curve, the prob. of recalling the price of good A is Pr(A)=m(A) and so for good B it would be Pr(B)=m(B). If the price of good A can triger recalling good B then the spreading activation incoporated prob. of recalling good B becomes Pr(B|A) so =Pr(A int B)/Pr(A). Since spreading activation helped recalling thr price of good B I assume Pr(B|A)>Pr(B).
Thanks for your comments on the readings,
Char
Sorry I forgot another question. Why are psi and lambda slightly different for each person? Why slightly but not a huge difference between, say, a young man and an old person?
ReplyDeleteAnonymous,
ReplyDeleteAgain, I may not be the best person to ask. First, I assume "Pr(B|A)" means probability of B given A. Second, I don't know what "Pr(A int B)" means. I have had some statistics, but not very advanced.
It seems a reasonable hypothesis that Pr(B|A)>Pr(B) if and only if the neurons which encode A are nearby and interrelated with the neurons that encode B. Remember, the brain is not some magic black box where everything you think may be related is actually interconnected within it. The brain does not search through a database of all possible related items. Instead, only if a memory was created in a way that was related to another memory will it necessarily be "activated" by that other memory. And, even then, with perhaps decreasing likelihood over time. Remember, the forgetting curve is not caused by memories vaporizing into thin air. It is caused by dozens - perhaps thousands - of synapses decreasing in strength over time and eventually disappearing altogether. (Reread the section of my paper under the heading "'The Power Law' as an Emergent Property" to see how the exponential degradation of all those different synapses creates the power function when they are all combined.
Now, consider that the phenomenon of one memory A being related to a memory B, such that A can activate B, is entirely a function of a cross connection of neurons connected by synapses. All those synapses will degrade according to their own individual strength and fragility. Therefore, the ability of A to activate B will also degrade following it's own individual power function.
In addition to A activating B directly, there will also be untold other factors which work to activate both A and B to varrying degrees. So, for any given memories A and B, it may be impossible to tell how much of the activation of B was due to the activation of A and how much of it was due to other factors which just happen work to activate both A and B independently. Remember, everyone's associations of A and B will be different depending on the circumstances under which A and B were formed. Remember, too, that testing for the strength of the relationship between A and B subsequently strenthens that relationship.
(continued in next comment)
(Continued from previous comment)
ReplyDeleteOne would have to design an experiment wherein dozens of relationships between various pairs of memories were created under identical situations and then measure Pr(B(sub i)) - Pr(B(sub i)|A(sub i)) for dozens of i all under identical situations and over different time frames, in order to get any idea as to a general rule for this "spreading activation" theory. In the end it would be like physics - wherein one has to simplify situations to the point of being unrealistic in order to use any of the basic mathematical equations given to us in physics class. The formulas and relationships derived from the above experimentation would only be useful within an incredibly controlled situation. I believe it would be the kind of thing that - by its very nature - would not be useful outside of the laboratory.
Finally, in your situation, a shopper's memory of price Q may likely be influenced by the memories of A through P, but confounded by their memories of prices in other stores and during sales which are no longer in effect.
I believe a more likely hypothesis is that shoppers build up a general perception over time as they shop, which is stored as an entirely separate memory from all the prices they have seen. When you ask subjects to forcast future inflation, they are not calculating anything in their head at all. Instead, they are merely drawing upon the perception they have already developed over time. Unfortunately, as research has shown, people are not always aware of their existing perceptions. In addition, when asked about how they came to the answers they give, people often conjure up a calculation on the spot in an attempt to justify the perception they have developed over time - even though they have no recollection of developing the perception or how it got there. This phenomenon can often confuse aspiring researchers into believing what the subjects believe, that they really are making calculations based upon their recollection of specific facts such as price information.
Oh, yeah, lambda and psi are not necessarily only "slightly" different between different people. In fact, I believe they may vary widely between different people and between different subjects within the same person. However, barring drastic deficiencies due to abnormal brain chemistry or development, and given similar learning conditions, all values of psi and lambda should fall within a certain range due to the similarity of neurobiology across the species.
ReplyDeleteRemember, lambda and psi are functions of the strength and fragility, respectively, of any particular memory. The strength and fragility are in turn functions of the number of synapses which have been established for a particular memory and how well each of those individual synapses have been reinforced, thus reducing their rate of degradation as per my other paper mentioned earlier.
This maybe a dead thread given the date....but, just in case, I'll pose a question. Have you come across any research using a delayed match-to-sample formulation using 3 stimuli?
ReplyDeleteYou are correct. It has been a very, very long time since I wrote this paper. Also keep in mind that I am NOT a researcher working in this field. I just did secondary research and read a hell of a lot of papers and then distilled them down into this paper. I do recall some research on delayed match-to-sample but I do not recall if any of them used three stimuli. I discounted match-to-sample because I do not consider it true recall. It is far too easy for one's brain to fool one's self into believing that one actually recalls a sample when one does not, even if one has actually seen that sample. There is no way that I know of for a researcher to differentiate between these two conditions reliably. Besides, most useful learning means the ability to recall something when it is NOT being presented to you, not merely recognizing it when it is being presented. The latter may help on multiple choice tests, but not much in real life. At least not reliably.
DeleteThank you so much for your prompt reply and feedback!! I agree, the 'real life' aspect is lacking, although the math is interesting :) Thank you again!
Delete